벡터는 선형 대수학의 기본 요소입니다. 벡터는 머신러닝 분야에서 알고리즘을 훈련할 때 대상 변수(y)와 같은 알고리즘 및 프로세스에 대한 설명에 사용됩니다. 이 튜토리얼에서는 머신러닝을 위한 선형 대수 벡터를 발견합니다. 이 자습서를 완료하면 다음을 알 수 있습니다. 벡터가 무엇이며 NumPy를 사용하여 파이썬에서 벡터를 정의하는 방법. 덧셈, 뺄셈, 곱셈 및 나눗셈과 같은 벡터 산술을 수행하는 방법. 내적 및 […]
머신러닝 데이터는 배열로 표시됩니다. 파이썬에서 데이터는 거의 보편적으로 NumPy 배열로 표현됩니다. Python을 처음 사용하는 경우 네거티브 인덱싱 및 배열 슬라이싱과 같은 데이터에 액세스하는 몇 가지 Python 방법에 혼란스러울 수 있습니다. 이 자습서에서는 NumPy 배열(array)에서 데이터를 올바르게 조작하고 액세스하는 방법을 배웁니다. 이 자습서를 완료하면 다음을 알 수 있습니다. 목록 데이터를 NumPy 배열로 변환하는 방법. Pythonic 인덱싱 및 슬라이싱을 […]
배열은 머신러닝에 사용되는 기본 데이터 구조입니다. 파이썬에서 N차원 배열 또는 ndarray라고 하는 NumPy 라이브러리의 배열은 데이터를 표현하기 위한 기본 데이터 구조로 사용됩니다. 이 튜토리얼에서는 숫자를 표현하고 Python에서 데이터를 조작하기 위한 NumPy의 N차원 배열을 발견하게 됩니다. 이 자습서를 완료하면 다음을 알 수 있습니다. ndarray가 무엇이며 파이썬에서 배열을 만들고 검사하는 방법. 새로운 빈 배열과 기본값이 있는 배열을 만들기 […]
선형 대수학은 많은 난해한 이론과 발견이 있는 큰 분야이지만 머신러닝 실무자에게는 현장에서 가져온 너트와 볼트 도구와 표기법이 필요합니다. 선형 대수학이 무엇인지에 대한 견고한 기초가 있으면 좋은 부분이나 관련 부분에만 집중할 수 있습니다. 이 집중 과정에서는 Python을 사용하여 머신러닝에 사용되는 선형 대수 표기법을 7일 만에 시작하고 자신 있게 읽고 구현하는 방법을 알아봅니다. 이 집중 코스는 누구를 […]
머신러닝을 시작하기 전에 선형 대수학을 배울 필요는 없지만 언젠가는 더 깊이 파고들고 싶을 수 있습니다. 사실, 수학의 한 영역에서 다른 영역보다 먼저 개선해야 할 것을 제안한다면, 그것은 선형 대수학일 것입니다. 선형 대수학은 머신러닝 알고리즘에 대한 더 나은 직관을 이해하고 구축하는 데 필요한 도구를 제공합니다. 이 게시물에서는 선형 대수학에 대해 자세히 살펴보고 머신러닝에서 더 많은 것을 […]
선형 대수학은 벡터, 행렬 및 선형 변환과 관련된 수학의 하위 분야입니다. 알고리즘 작동을 설명하는 데 사용되는 표기법에서 코드의 알고리즘 구현에 이르기까지 머신러닝 분야의 핵심 기반입니다. 선형 대수학은 머신러닝 분야에 필수적이지만 긴밀한 관계는 종종 벡터 공간이나 특정 행렬 연산과 같은 추상적 개념을 사용하여 설명되지 않습니다. 이 게시물에서는 선형 대수학을 사용하는 머신러닝의 10가지 일반적인 예를 발견하게 될 것입니다. 이 게시물을 […]
선형 대수학은 머신러닝에 대한 더 깊은 이해의 전제 조건으로 보편적으로 동의되는 수학 분야입니다. 선형 대수학은 많은 난해한 이론과 발견이 있는 큰 분야이지만 현장에서 가져온 너트와 볼트 도구와 표기법은 머신러닝 실무자에게 실용적입니다. 선형 대수학이 무엇인지에 대한 견고한 기초가 있으면 좋은 부분이나 관련 부분에만 집중할 수 있습니다. 이 튜토리얼에서는 머신러닝 관점에서 선형 대수학이 정확히 무엇인지 알아낼 것입니다. […]
데이터에 상한과 하한을 두는 것이 유용할 수 있습니다. 이러한 경계는 변칙을 식별하고 예상되는 사항에 대한 기대치를 설정하는 데 사용할 수 있습니다. 모집단의 관측치에 대한 한계를 공차 구간이라고 합니다. 공차 구간은 추정 통계량 필드에서 나옵니다. 공차 구간은 단일 예측값에 대한 불확실성을 정량화하는 예측 구간과 다릅니다. 또한 평균과 같은 모집단 모수의 불확실성을 정량화하는 신뢰 구간과도 다릅니다. 대신, 공차 구간은 […]
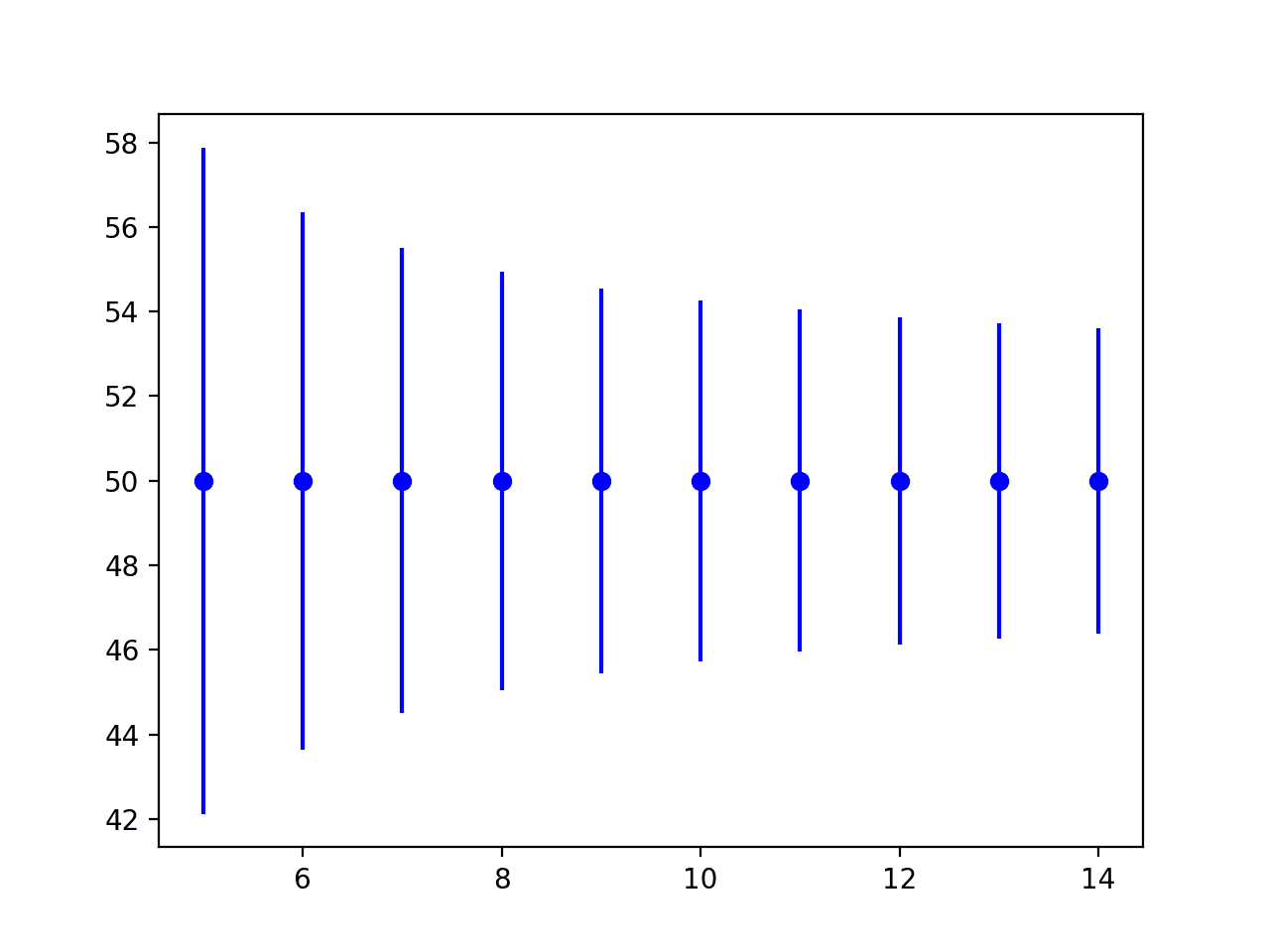
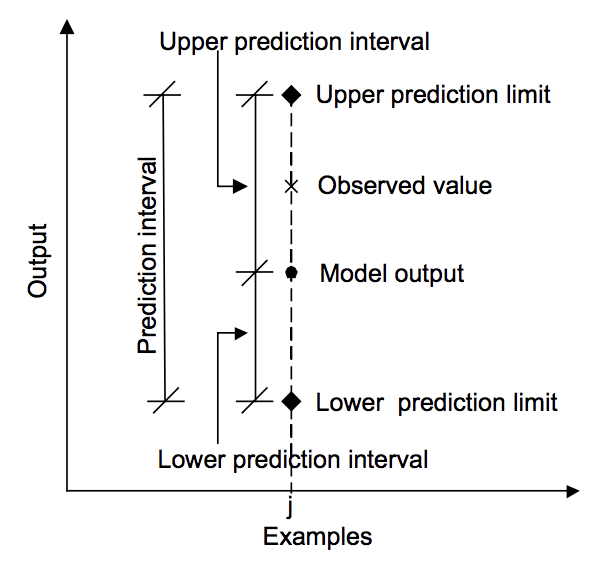
머신러닝 관점의 예측은 해당 예측의 불확실성을 숨깁니다. 예측 구간은 예측의 불확실성을 정량화하고 전달하는 방법을 제공합니다. 이는 대신 평균 또는 표준 편차와 같은 모집단 모수의 불확실성을 정량화하려는 신뢰 구간과 다릅니다. 예측 구간은 단일 특정 결과에 대한 불확실성을 설명합니다. 이 자습서에서는 예측 구간과 간단한 선형 회귀 모델에 대해 예측구간을 계산하는 방법을 알아봅니다. 이 자습서를 완료하면 다음을 알 […]
머신러닝의 대부분은 보이지 않는 데이터에 대한 머신러닝 알고리즘의 성능을 추정하는 것과 관련이 있습니다. 신뢰 구간은 추정치의 불확실성을 정량화하는 방법입니다. 모집단의 독립 관측치 표본에서 추정된 평균과 같은 모집단 모수에 한계 또는 발생가능성를 추가하는 데 사용할 수 있습니다. 신뢰 구간은 추정 통계량 필드에서 가져옵니다. 이 튜토리얼에서는 신뢰 구간과 실제로 신뢰 구간을 계산하는 방법을 알아봅니다. 이 자습서를 완료하면 다음을 알 […]