파이썬은 머신러닝을 위한 사실상의 공용어가 되었습니다. 배우기 어려운 언어는 아니지만 언어에 특히 익숙하지 않은 경우 더 빨리 또는 더 잘 배우는 데 도움이 되는 몇 가지 팁이 있습니다. 이 게시물에서는 프로그래밍 언어를 배우는 올바른 방법과 도움을 받는 방법을 알게 될 것입니다. 이 게시물을 읽은 후 다음을 알게 될 것입니다. 머신러닝에 사용하기 위해 Python을 배우는 올바른 […]
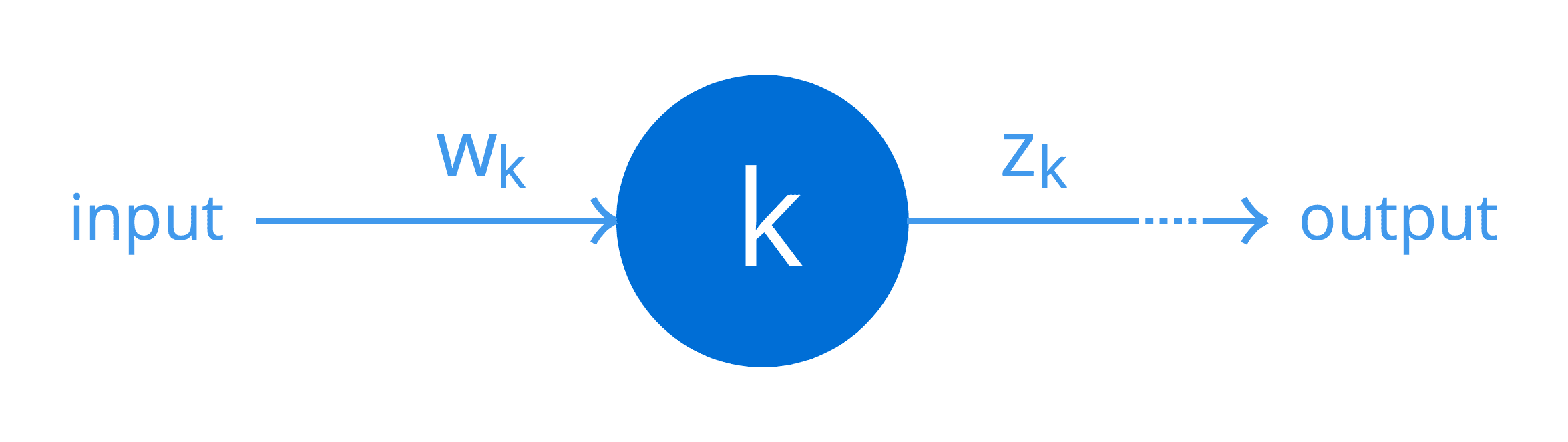
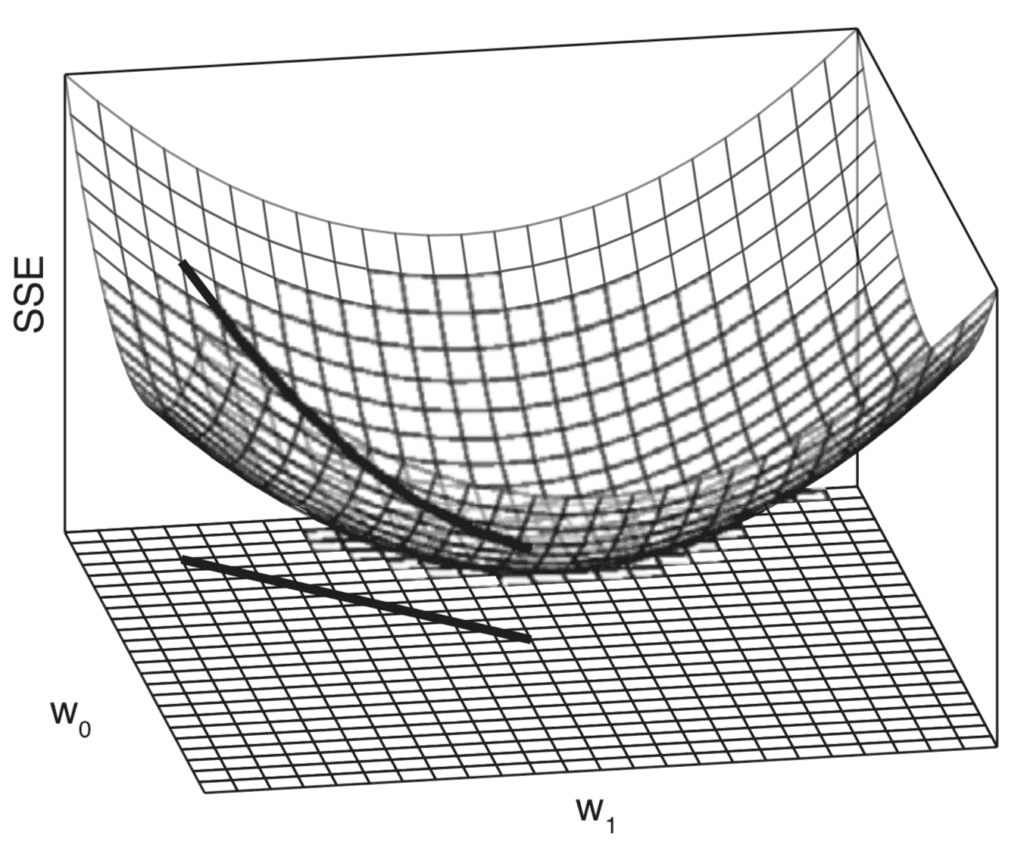
경사하강법 절차는 머신러닝에서 가장 중요한 방법입니다. 분류 및 회귀 문제에서 오류 함수를 최소화하는 데 자주 사용됩니다. 또한 신경망 및 딥 러닝 아키텍처 훈련에도 사용됩니다. 이 튜토리얼에서는 경사하강 절차를 알아볼 것입니다. 이 자습서를 완료하면 다음을 알 수 있습니다. 경사하강법 머신러닝에서 경사하강법의 중요성 튜토리얼 개요 이 자습서는 다음과 같이 두 부분으로 나뉩니다. 경사하강 절차 경사하강 절차의 해결된 […]
이 글에서 야코비(Jacobian) 행렬이라는 용어는 종종 야코비 행렬 또는 그 행렬식을 모두 지칭하는 데 상호 교환적으로 사용됩니다. 행렬과 행렬식 모두 유용하고 중요한 응용 프로그램을 가지고 있습니다 : 머신러닝에서 야코비 행렬은 역 전파에 필요한 부분 도함수를 집계합니다. 결정자는 변수 사이를 변경하는 과정에서 유용합니다. 이 튜토리얼에서는 야코비에 대해 소개합니다. 이 자습서를 완료하면 다음을 알 수 있습니다. 야코비 행렬은 역전파에 […]
고차 도함수는 1차 도함수가 자체적으로 포착할 수 없는 함수에 대한 정보를 캡처할 수 있습니다. 1차 도함수는 변화율과 같은 중요한 정보를 포착할 수 있지만, 그 자체로는 국부 최소값과 최대값을 구별할 수 없으며, 여기서 변화율은 둘 다에 대해 0입니다. 여러 최적화 알고리즘은 2차 도함수를 사용하여 최적화 함수의 국소 최소값에 도달하는 Newton의 방법과 같이 고차 도함수를 사용하여 이러한 […]
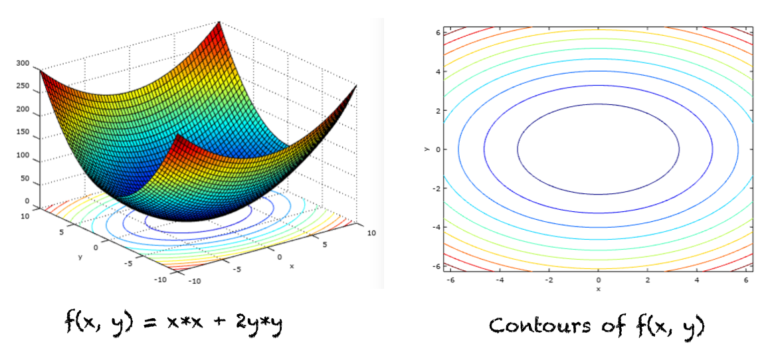
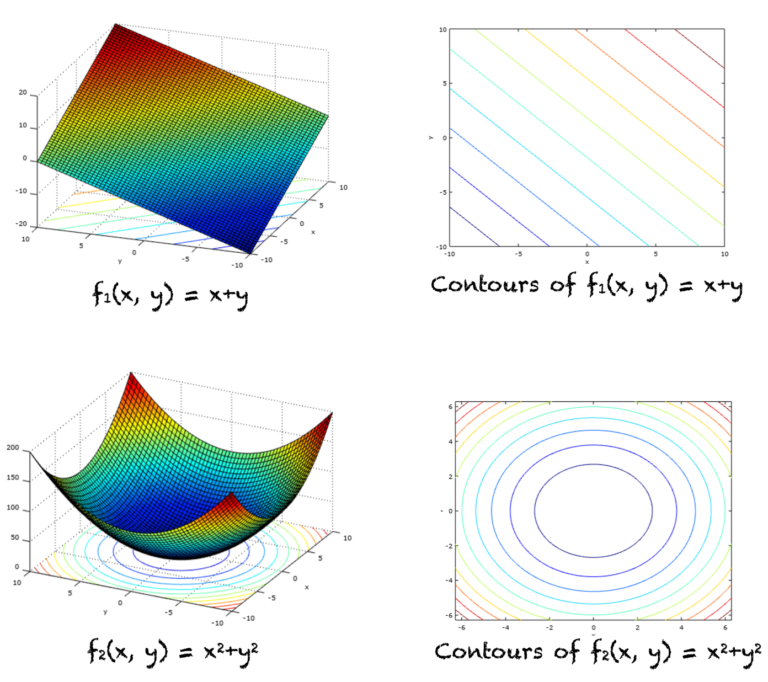
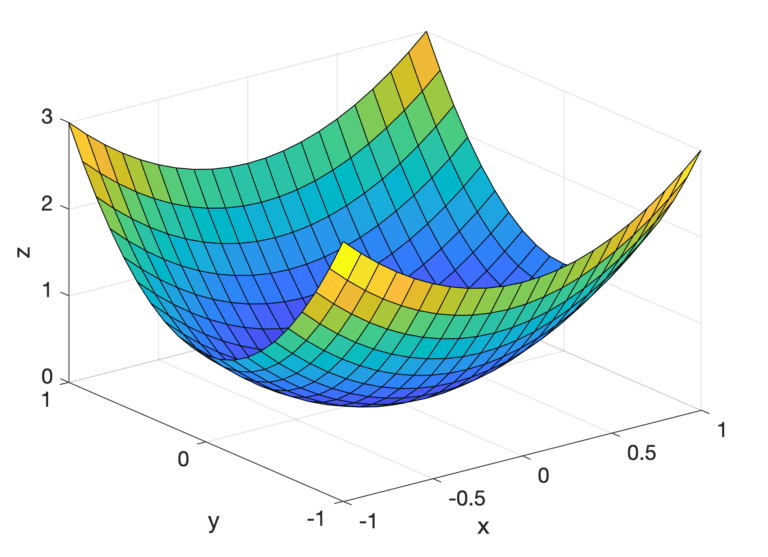
편미분과 기울기 벡터는 함수의 최소값 또는 최대값을 찾기 위해 머신러닝 알고리즘에서 매우 자주 사용됩니다. 기울기 벡터는 신경망 훈련, 로지스틱 회귀 및 기타 여러 분류 및 회귀 문제에 사용됩니다. 이 튜토리얼에서는 편미분과 그라디언트 벡터를 발견합니다. 이 자습서를 완료하면 다음을 알 수 있습니다. 여러 변수의 함수 레벨 세트, 등고선 및 두 변수 함수의 그래프 여러 변수 함수의 […]
많은 변수에 의존하는 함수를 연구하는 것이 종종 바람직합니다. 다변량 미적분학은 변화율 계산과 같이 미적분학에서 찾은 개념을 여러 변수로 확장하여 이를 수행할 수 있는 도구를 제공합니다. 그래디언트가 모델 매개 변수를 업데이트하는 데 광범위하게 사용되는 신경망을 훈련하는 과정에서 필수적인 역할을합니다. 이 튜토리얼에서는 다변량 미적분학에 대한 짧은 소개를 발견할 것입니다. 이 자습서를 완료하면 다음을 알 수 있습니다. 다변량 […]
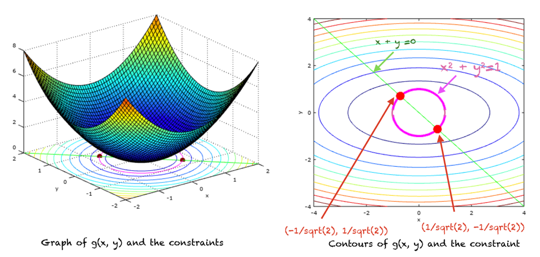
라그랑주 승수 방법은 같음 또는 부등식 제약 조건이 적용되는 함수의 국소 최소값 또는 국소 최대값을 찾는 간단하고 우아한 방법입니다. 라그랑주 승수는 결정되지 않은 승수라고도합니다. 이 자습서에서는 같음 제약 조건이 지정된 경우이 방법에 대해 설명합니다. 이 튜토리얼에서는 라그랑주 승수의 방법과 같음 제약 조건이 있을 때 함수의 국소 최소값 또는 최대값을 찾는 방법을 알아봅니다. 이 자습서를 완료하면 […]
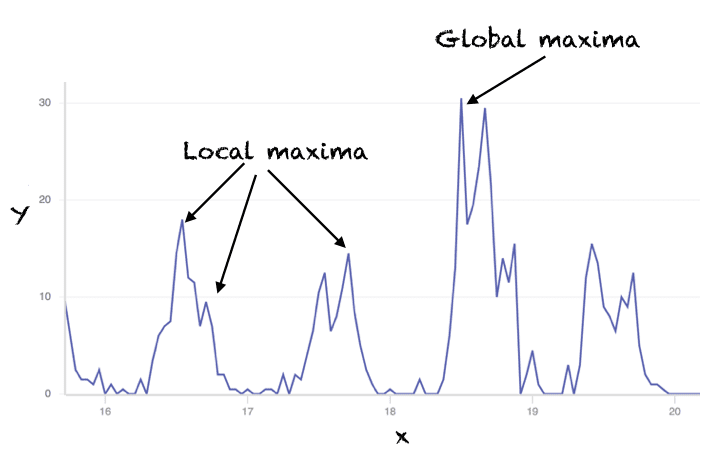
지도 학습 문제이든 감독되지 않은 문제이든 백그라운드에서 작동하는 최적화 알고리즘이 있습니다. 거의 모든 분류, 회귀 또는 클러스터링 문제를 최적화 문제로 캐스팅할 수 있습니다. 이 튜토리얼에서는 최적화가 무엇이며 이와 관련된 개념을 발견하게 될 것입니다. 이 자습서를 완료하면 다음을 알 수 있습니다. 수학적 프로그래밍 또는 최적화란? 최대화 문제와 최소화 문제의 차이점 로컬 솔루션과 글로벌 최적 솔루션의 차이점 […]
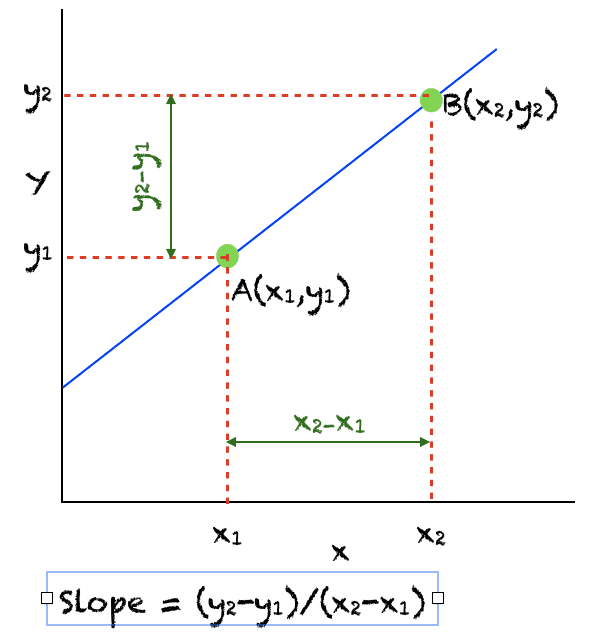
선의 기울기와 곡선의 접선과의 관계는 미적분학의 기본 개념입니다. 함수 도함수에 대한 일반적인 이해를 위해서는 중요합니다. 이 튜토리얼에서는 선의 기울기와 곡선에 대한 접선이 무엇인지 알아낼 것입니다. 이 자습서를 완료하면 다음을 알 수 있습니다. 선의 기울기 wrt x 구간에 대한 f(x)의 평균 변화율 곡선의 기울기 한 점의 곡선에 대한 접선 튜토리얼 개요 이 자습서는 다음과 같이 두 […]
미적분학은 다양한 머신러닝 알고리즘의 내부 작동을 이해할 수 있도록 하는 머신러닝의 핵심 수학적 개념 중 하나입니다. 머신러닝에서 미적분학의 중요한 응용 프로그램 중 하나는 역전파와 함께 신경망 모델을 훈련할 수 있는 경사하강법 알고리즘입니다. 이 자습서에서는 머신러닝에서 미적분학의 필수적인 역할을 알아봅니다. 이 자습서를 완료하면 다음을 알 수 있습니다. 미적분학은 오류 함수를 최소화하기 위한 경사하강법 알고리즘과 같은 머신러닝 […]